はじめに
こんにちは、クラウド事業部の丸山です。
本連載では「私たちの生活を密かに守っている暗号技術の仕組みと歴史」について、エンジニア視点で解説しています。
第4回となる今回は、前回解説した共通鍵暗号の課題を解決した「公開鍵暗号」の革命的概念について解説します。
インターネットセキュリティの根幹を支える非対称暗号の原理から、そのインパクトまでの技術の進化を探ります。
共通鍵暗号の限界 - 鍵配送問題
前回解説したDESやAESなどの共通鍵暗号は、暗号化と復号に同じ鍵を使用します。
この方式の最大の課題は「鍵配送問題」でした。
- 通信を始める前に、両者が同じ鍵を安全に共有する必要がある
- 盗聴される可能性のある通信路では、鍵自体を安全に送ることができない
- 多数の相手と安全に通信するには、相手ごとに異なる鍵を管理する必要がある
この一見解決不可能に思える問題に、1970年代後半に革命的な解決策が登場します。
共通鍵暗号と鍵配送問題の図解
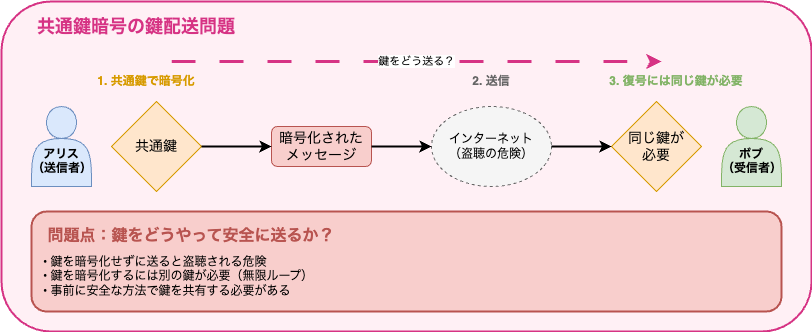
上の図のように、アリスとボブが安全に通信するには同じ鍵を持つ必要がありますが、
その鍵を安全に交換する方法がないという「鶏と卵」のような問題が存在していました。
公開鍵暗号の革命
1976年、スタンフォード大学のWhitfield DiffieとMartin Hellmanが「公開鍵暗号」の概念を発表しました。
この画期的なアイデアは、暗号の世界に根本的な変革をもたらします。
公開鍵暗号の基本原理
公開鍵暗号は、「暗号化と復号に異なる鍵を使用する」という革命的な概念に基づいています。
- 公開鍵:誰にでも公開できる鍵。この鍵で暗号化されたメッセージは、対応する秘密鍵でのみ復号可能
- 秘密鍵:自分だけが所有する鍵。対応する公開鍵で暗号化されたメッセージを復号できる
この仕組みにより、秘密の鍵を事前に共有することなく、安全な通信が可能になりました。
南京錠のアナロジーで理解する公開鍵暗号
公開鍵暗号の仕組みは、南京錠を使って分かりやすく説明できます。
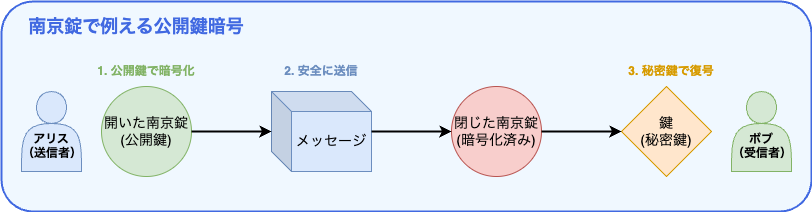
- ボブは「開いた南京錠」(公開鍵)を多数作り、誰にでも配布します
- アリスはメッセージを箱に入れ、ボブから受け取った南京錠でロックします(暗号化)
- 一度ロックされた南京錠は、ボブが持っている特別な鍵(秘密鍵)でしか開けられません
- ボブは受け取った箱を秘密鍵で開錠し、メッセージを取り出します(復号)
この方法なら、誰でも「ボブだけが開けられる箱」を作れますが、開けられるのはボブだけです。
南京錠(公開鍵)は公開しても安全なのです。
ディフィー・ヘルマン鍵交換 - 安全な鍵の共有
公開鍵暗号の最初の実用的なアプリケーションは、「ディフィー・ヘルマン鍵交換」です。
これは暗号化アルゴリズムではなく、盗聴される可能性のある通信路上で安全に共通鍵を確立するための方法です。
色の混合で理解するディフィー・ヘルマン鍵交換
ディフィー・ヘルマン鍵交換の仕組みは、数学的には複雑ですが、「色の混合」という例えを使うと直感的に理解できます。
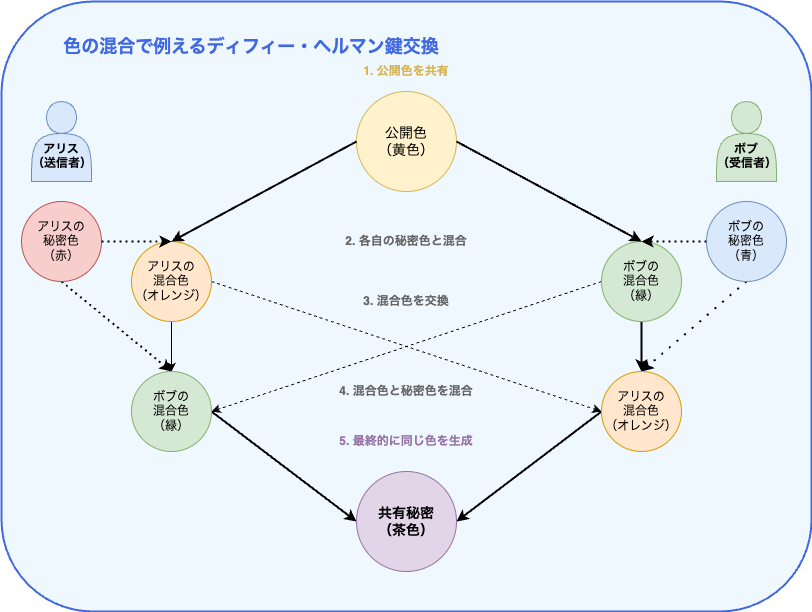
- アリスとボブは公開の場で「黄色」という共通の色(公開パラメータ)に合意します
- アリスは秘密の「赤色」(秘密鍵a)を選び、黄色と混ぜて「オレンジ色」(公開鍵A)を作り、ボブに送ります
- ボブは秘密の「青色」(秘密鍵b)を選び、黄色と混ぜて「緑色」(公開鍵B)を作り、アリスに送ります
- アリスはボブから受け取った「緑色」に自分の秘密の「赤色」を混ぜます
- ボブはアリスから受け取った「オレンジ色」に自分の秘密の「青色」を混ぜます
- アリスとボブは両方とも「茶色」という同じ色(共有秘密)を得ます
ここで重要なのは、盗聴者がオレンジ色と緑色を見ても、元の赤色と青色を分離することは事実上不可能なため、最終的な茶色を作れないということです。これが「一方向性関数」の本質です。
ディフィー・ヘルマン鍵交換の仕組み
ディフィー・ヘルマン鍵交換は、「一方向性関数」という性質を使って、安全に共通の鍵(共通鍵)を作る仕組みです。
アリスとボブは、共通のルール(ある数字の組み合わせ)にあらかじめ同意しておきます。
そして、それぞれが「自分だけの秘密の数」を使って、お互いに情報をやり取りします。
- アリスとボブは、共通の設定(数字のセット)をあらかじめ決めておきます。
- アリスは、自分だけが知っている秘密の数を使って、公開してもよい情報を作り、ボブに送ります。
- ボブも同じように、自分の秘密の数を使って、アリスに公開情報を送ります。
- アリスは、ボブから受け取った情報と自分の秘密を使って、共通の鍵を計算します。
- ボブも同様に、アリスから受け取った情報と自分の秘密を使って、同じ共通の鍵を計算します。
こうして、お互いに秘密の数字を教え合うことなく、同じ共通鍵を持つことができます。 途中でやり取りされる情報を誰かが盗み見たとしても、「元の秘密」を逆算するのは非常に難しく、同じ鍵を作ることはほぼ不可能です。
離散対数問題の難しさ
ディフィー・ヘルマンが安全な理由は、「離散対数問題」と呼ばれる、逆向きの計算がとても難しいという数学的な性質にあります。
たとえば、「ある計算をしてこの答えが出た」という情報は簡単に作れますが、
「じゃあその計算に使われた元の数は何か?」を調べるのは、ものすごく大変です。
これは、以下のような特徴があります。
- 正しい鍵を使って「鍵をかける」のは簡単
- でも、鍵なしで「こじ開ける」のはとても難しい
現在のコンピューターでも、鍵に使われている数が十分に大きければ、この逆計算を現実的な時間内に解くことはできません。 この性質が、ディフィー・ヘルマンの安全性を支えています。
共通鍵暗号と公開鍵暗号の違い
ここで、共通鍵暗号と公開鍵暗号の根本的な違いを図解で比較してみましょう。
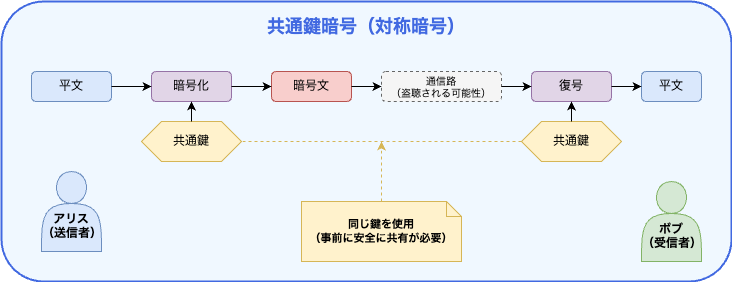
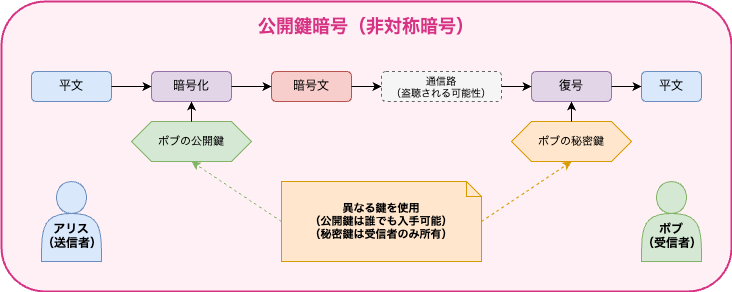
共通鍵暗号では、暗号化と復号に同じ鍵を使用するため、事前の秘密共有が必要です。
一方、公開鍵暗号では、暗号化には誰でも使える公開鍵を使い、復号には所有者だけが持つ秘密鍵を使うため、事前の秘密共有が不要になります。
RSA - 公開鍵暗号の代表格
1977年、Ron Rivest、Adi Shamir、Leonard Adlemanは、公開鍵暗号の最も有名な実装である「RSA」を発表しました。
RSAは、ディフィー・ヘルマンの概念を拡張し、実際のメッセージの暗号化・復号とデジタル署名を可能にしました。
郵便ポストで理解するRSA
RSAの仕組みを郵便ポストに例えると分かりやすくなります。
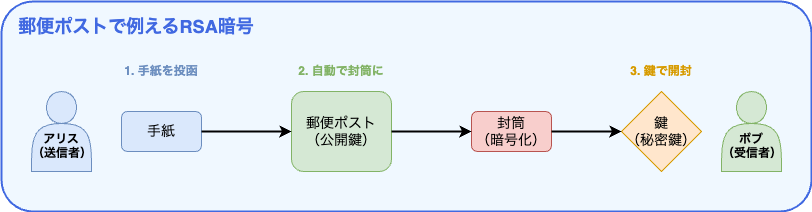
- ボブは特別な郵便ポスト(公開鍵)を作り、町中に設置します
- このポストは誰でも手紙を投函できますが、開けられるのはボブだけです
- アリスはメッセージをボブの郵便ポストに投函します(公開鍵で暗号化)
- ボブは自分だけが持つ鍵でポストを開け、メッセージを取り出します(秘密鍵で復号)
この例えのポイントは、「投函は誰でもできるが、取り出せるのは持ち主だけ」という非対称性にあります。
RSAの基本原理とプロセスフロー
RSAは「鍵ペア」という特別な仕組みを使った暗号方式です。
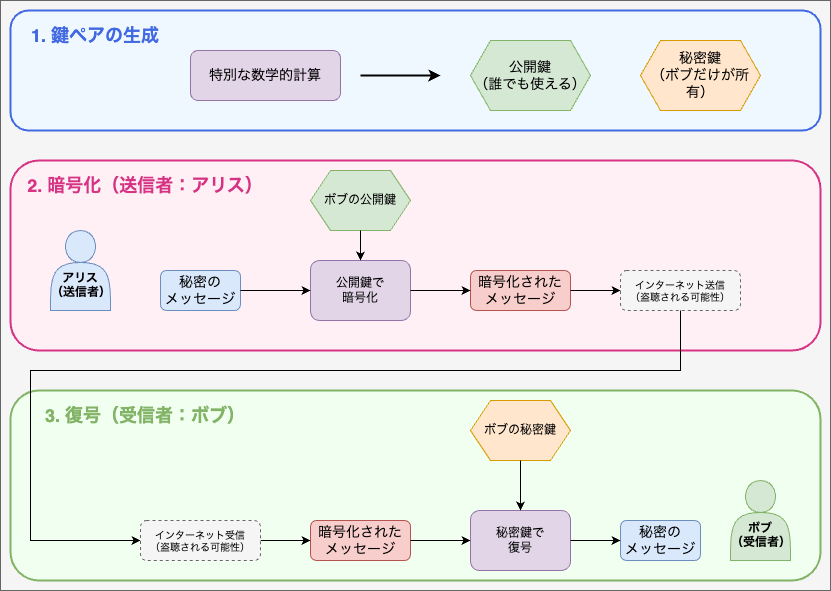
RSAの3つのステップ
鍵ペアの生成:
- 特別な数学的計算により、2つの鍵を作成
- 公開鍵:誰でも使える鍵(暗号化用)
- 秘密鍵:受信者だけが持つ鍵(復号用)
暗号化:
- 送信者(アリス)は受信者(ボブ)の公開鍵を使ってメッセージを暗号化
- 暗号化されたメッセージは、ボブの秘密鍵でしか復号できない
復号:
- 受信者(ボブ)は自分の秘密鍵を使って暗号化されたメッセージを復号
- 元の秘密メッセージが復元される
RSAの安全性の秘密
RSAの安全性は、「公開鍵から秘密鍵を計算するのが非常に困難」という性質に基づいています。
これは現在のコンピュータでは現実的に不可能な計算量が必要だからです。
実用的なメリット - 事前の鍵共有が不要(共通鍵暗号の課題を解決) - 公開鍵は自由に配布できる - 秘密鍵は受信者だけが管理すればよい
RSAの応用範囲
RSAは暗号化だけでなく、以下のような幅広い用途に使われています。
- デジタル署名: 秘密鍵で署名を生成し、公開鍵で検証可能
- 認証: 秘密鍵の所有を証明することで本人確認
- 鍵交換: 共通鍵暗号で使用する鍵の安全な交換
デジタル署名のプロセス
デジタル署名は公開鍵暗号のもう一つの重要な応用で、「暗号化の逆」の操作を行います。
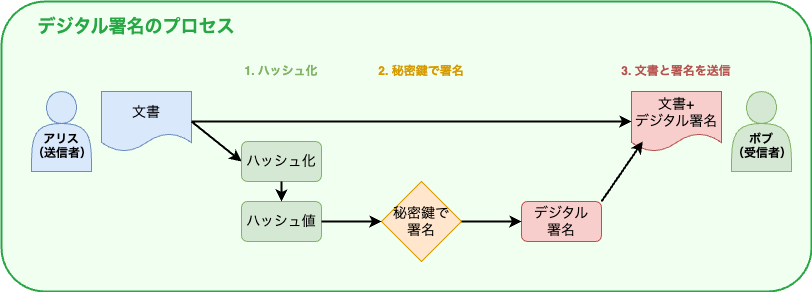
- 送信者は文書のハッシュ値を計算
- このハッシュ値を自分の秘密鍵で暗号化(署名を生成)
- 文書と署名を受信者に送信
- 受信者は送信者の公開鍵で署名を復号し、ハッシュ値を取得
- 受信者は受け取った文書からハッシュ値を計算し、署名から得たハッシュ値と比較
- 一致すれば、文書は確かに署名者が作成し、途中で改ざんされていないことが証明される
これは実印による捺印に似ていますが、デジタル署名は文書の内容と密接に結びついているため、改ざんを検出できる点がさらに優れています。
公開鍵基盤(PKI)
RSAなどの公開鍵暗号を実用的に運用するために、「公開鍵基盤」(Public Key Infrastructure, PKI)が構築されています。
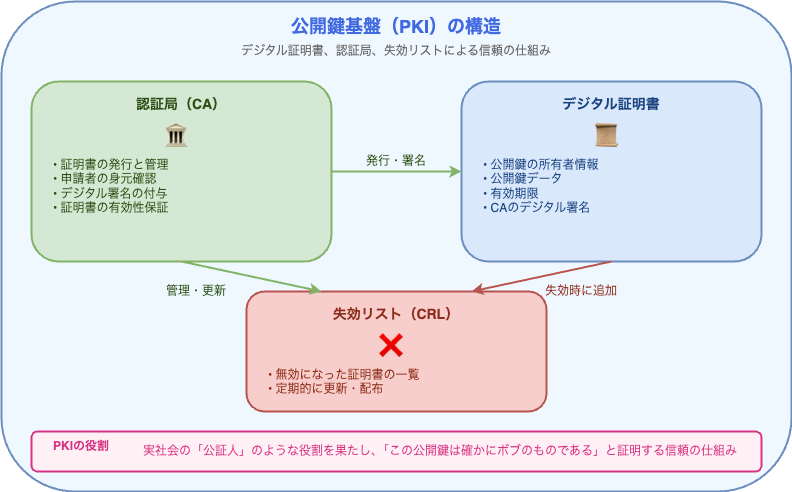
- デジタル証明書: 公開鍵の所有者を証明
- 認証局(CA): 証明書の発行と管理
- 失効リスト(CRL): 無効になった証明書の一覧
PKIは、インターネットの安全性を支える重要なインフラストラクチャとなっています。
認証局は、実社会の「公証人」のような役割を果たし、「この公開鍵は確かにボブのものである」と証明します。
デモ:RSA暗号の原理を体験
RSA暗号の基本原理を簡略化したデモを通じて、公開鍵暗号の仕組みを体験してみましょう。
RSA鍵生成(教育用の小さい数字)
RSA暗号化
RSA復号
注: このデモは教育目的であり、使用している数値は非常に小さいため実用的ではありません。実際のRSAは1024ビット以上の非常に大きな数を使用します。
RSAの安全性と鍵長
このデモでは小さな数値を使用していますが、実際のRSAは非常に大きな数値を使います。
- 1990年代: 512ビット鍵
- 2000年代初頭: 1024ビット鍵
- 現在: 2048〜4096ビット鍵が推奨
鍵長が長くなるほど安全性は高まりますが、計算コストも増加します。
そのため、前述のハイブリッドアプローチが広く採用されています。
現代の暗号利用 - ハイブリッドアプローチ
現代のセキュアな通信では、公開鍵暗号と共通鍵暗号を組み合わせて使用する「ハイブリッドアプローチ」が標準的です。
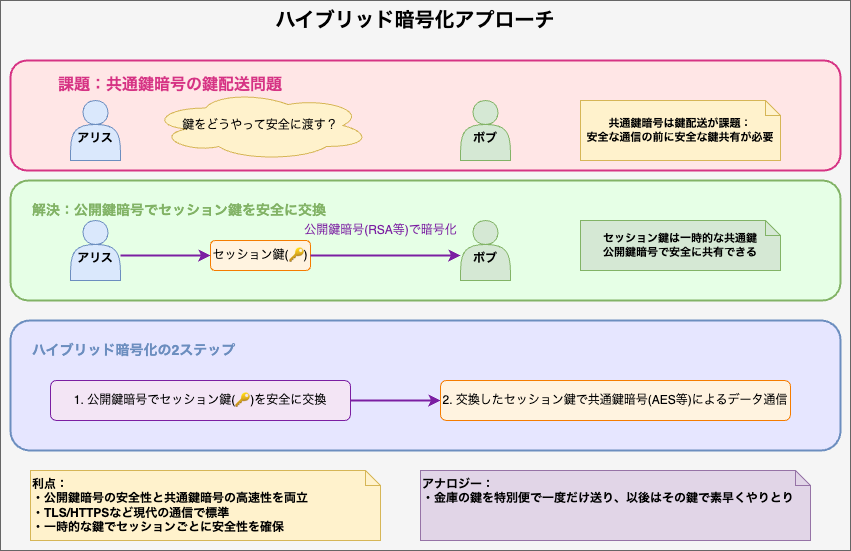
- 公開鍵暗号(RSAなど)で一時的な共通鍵(セッション鍵)を安全に交換
- 交換した共通鍵を使って、共通鍵暗号(AESなど)で実際のデータを暗号化
この方式により、公開鍵暗号の安全性と共通鍵暗号の処理効率の両方を活かしています。
例えば、HTTPSの通信では以下のような仕組みとなります。
- TLSハンドシェイクにおいて、RSAや楕円曲線暗号を使って一時的な共通鍵を共有
- その後の通信は、共有した鍵を使ってAESなどの高速な共通鍵暗号で保護
これは「安全な金庫の鍵を特別便で一度だけ送り、以後の通信はその鍵で素早く暗号化する」というアプローチに似ています。
まとめ
本章では、共通鍵暗号の鍵配送問題を解決した公開鍵暗号の革命的概念と、RSAの基本原理を解説しました。
公開鍵暗号は、「暗号化と復号に異なる鍵を使う」というアイデアで、事前の秘密共有なしに安全な通信を可能にしました。
この技術はデジタル署名や認証など、現代のインターネットセキュリティの根幹を支えています。
本連載では、暗号技術の歴史的な進化とその本質、そして現代のセキュア通信を支えるハイブリッドアプローチまでを体系的に解説してきました。 暗号は、私たちの生活のあらゆる場面で密かに活躍しています。 ひとまず本シリーズはここで一区切りとしますが、もし機会があれば「現代社会での暗号化技術の応用」や「量子コンピュータ時代の新しい暗号」など、より実践的・未来的な話題もご紹介できればと思います。 ここまでお読みいただき、ありがとうございました!
おわりに
私達クラウド事業部はクラウド技術を活用したSI/SESのご支援をしております。
また、一緒に働いていただける仲間も募集中です! ご興味持っていただけましたらぜひお声がけください。